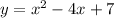Question

PLEASE HELP

Write the quadratic equation in standard form that represents the table below:
x y

-2 19

-1 12

0 7

1 4

f(x)=

Answer 1

Explanation:

You have 3 unknowns: a, b, and c. It's our job to find them algebraically. I'm going to start with the point where x = 0 and y = 7. You'll see why in a minute. Filling in the standard form of a quadratic

`y=ax^2+bx+c` using (0, 7):

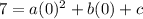`7=a(0)^2+b(0)+c` gives you that c = 7. We will use that value now when we write the next 2 equations. Now the point (-2, 19):

`19=a(-2)^2+b(-2)+7` and

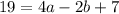`19=4a-2b+7` so

12 = 4a - 2b

Now for the next point (-1, 12):

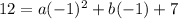`12=a(-1)^2+b(-1)+7` and

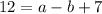`12=a-b+7` so

5 = a - b

Now we have a system of equations (the 2 bold font equations) that we will solve by elimination:

12 = 4a - 2b

5 = a - b

Multiply the bottom equation by -4 to get a new system:

12 = 4a - 2b

-20 = -4a + 4b

Add those together to get rid of the a terms and end up with

-8 = 2b so

b = -4

Now we can sub in -4 for b to solve for a. I'm using the second bold type equation to do this:

5 = a - (-4) and

5 = a + 4 so

a = 1 and the equation for the quadratic function is

`y=x^2-4x+7`