Question

The function f(x)=50⋅0.8x models the number of ants in Jonathan's ant farm after it is stricken by a deadly ant disease, where x represents the number of weeks since the first ant became sick. Which of the following are true statements? Select all that apply.

1. The function models exponential decay.

2. The function models exponential growth.

3. 50 represents the number of ants that die each week.

4. 50 represents the initial number of ants in the colony.

5. Two weeks after the initial ant became sick, there are only 32 ants remaining in the colony.

6. Eight weeks after the initial ant became sick, there are only 10 ants remaining in the colony.

Answer 1

1, 4, 5

Explanation:

0.8 < 1

So it's a decay

50(0.8^x)

At x = 0, it's 50 (initial)

50(0.8²)

32

Answer 2

Explanation:

In the exponential growth/decay function

`y=a(b)^x`, in our situation,

y is the number of ants remaining in the colony after the growth or decay,

a is the initial number of ants in the colony, and

b is the growth/decay rate. Rule: if b is greater than 1, the function is growth; if b is greater than 0 but less than 1, the function is decay.

Our equation looks like this (it's given):

`y=50(.8)^x`

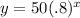
a = 50, which is the initial number of ants in the colony.

b = .8 (which actually means that then number of ants is declining by 20% each week). Since .8 is a fraction of 1, this is decay.

So far, we know that 1 and 4 are true. Let's look at 5. We have to do some solving to find out if it's true or not. If the number of ants after x = 2 weeks is 32, then we plug in 2 for x and see if the y we get as the answer is 32:

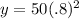`y=50(.8)^2` and

y = 50(.64) so

y = 32

5 is true as well. Let's test 6 by replacing x with 8 and seeing if y = 10:

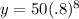`y=50(.8)^8` and

y = 50(.16777216) so

y = 8.388

6 is not true.

1, 4, 5 are true