Question

The radius of the cone is 1.25 inches, and its height is 2.75 inches. If the diameter of the bubble gum ball is 0.5 inches, what is the closest approximation of the volume of the cone that can be filled with flavored ice?

Answer 1

Step-by-step explanation:

The volume of a cone can be found as:

`V=(1)/(3)\pi r^2 h \\ \\ \\ Where: \\ \\ V:Volume \\ \\ r:radius \ of \ base \\ \\ h:height`

Given the radius and height, we can find the volume of the cone:

`V=(1)/(3)\pi r^2 h \\ \\ V=(1)/(3)\pi (1.25)^2(2.75) \\ \\ V=(1)/(3)\pi(1.5625)(2.75) \\ \\ V\approx 4.5in^3`

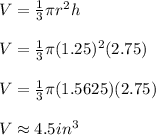
The volume of a sphere is:

`V=(4)/(3)\pi r^3 \\ \\ \text{Each gum ball has a diameter of 0.5in, so the radius is:} \\ \\ r=(0.5)/(2)=0.25in`

So, for each gum ball the volume is:

`V=(4)/(3)\pi r^3 \\ \\ V=(4)/(3)\pi (0.25)^3 \\ \\ V=0.065in^3`

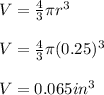
Therefore, the he closest approximation of the volume of the cone that can be filled with flavored ice is:

`4.5-0.065=4.43in^3`

Conclusion: The volume of the cone that can be filled with flavored ice is 4.43 cubic inches.