Answer:
C. √2 - 1
Explanation:
If we draw a square from the center of the large circle to the center of one of the small circles, we can see that the sides of the square are equal to the radius of the small circle (see attached diagram)
Let r = the radius of the small circle
Using Pythagoras' Theorem
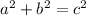
(where a and b are the legs, and c is the hypotenuse, of a right triangle)
to find the diagonal of the square:
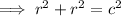
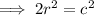
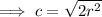
So the diagonal of the square =
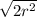
We are told that the radius of the large circle is 1:
⇒ Diagonal of square + r = 1
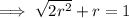
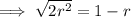
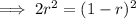
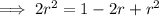

Using the quadratic formula to calculate r:

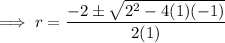
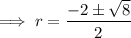
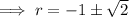
As distance is positive,
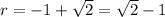 only
only