The sine of angle C is approximately 0.799, and the measure of angle C is 53.0° when rounded to the nearest tenth. therefore, option B is correct
To find the measure of angle
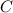 in triangle
in triangle
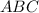 , we will use the Law of Sines, which states that in any triangle, the ratio of the length of a side to the sine of its opposite angle is constant. That is:
, we will use the Law of Sines, which states that in any triangle, the ratio of the length of a side to the sine of its opposite angle is constant. That is:
![\[ (a)/(\sin(A)) = (b)/(\sin(B)) = (c)/(\sin(C)) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/kqv3w87d57setl7n8ohz0628kbs8u347mz.png)
Where a,b and c are the lengths of the sides of the triangle, and A,B and C are the angles opposite those sides, respectively.
Given:
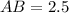
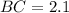
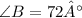
We want to find

Using the Law of Sines, we can set up the following equation:
![\[ (AB)/(\sin(B)) = (BC)/(\sin(C)) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/irpqk3i7zd8b2mwr9ykpae9uga30rfvs5k.png)
![\[ (2.5)/(\sin(72°)) = (2.1)/(\sin(C)) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/hu9zpkz5oof686xhbaqqs16imu7iwc059q.png)
Solving for \( \sin(C) \), we get:
![\[ \sin(C) = (2.1 \cdot \sin(72°))/(2.5) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/aro5e01lyzyuk25fm79exbvf99qb5l1ikq.png)
Let's calculate the value of
 and then find
and then find
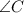 by taking the inverse sine.
by taking the inverse sine.
The sine of angle C is approximately 0.799, and the measure of angle C is 53.0° when rounded to the nearest tenth.