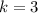Question

A quantity h varies directly with w and inversely with pIf h = 2, w = 4, and p = 6What is the constant of variation?

Answer 1

Value of constant of variation is
`k=3`

Explanation:

Let 'k' be the constant of variation.

According to first condition, h varies directly with w. That is,

`h\propto w`

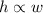
According to second condition, h varies inversely with p. That is,

`h\propto (1)/(p)`

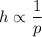
Combining both conditions,

`h\propto (w)/(p)`

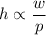
Now to remove proportionality sign use constant of variation k,

`h=k(w)/(p)`

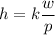
Given that, h = 2, w = 4 and p = 6. Substituting the value,

`2=k(4)/(6)`

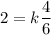
Multiplying both side of equation by
`(6)/(4)`

`(6)/(4)* 2=k`

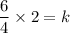
Simplifying,

`(12)/(4)=k`

`3=k`

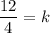
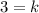
Therefore value of constant of variation is
`k = 3`