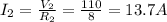Question

PLEASE HELP ASAP.

1. A series circuit contains an electric generator, three devices operated by electricity, and the necessary connecting wires. The resistances of the three devices are 20 ohms, 8 ohms, and 4 ohms. The resistance of the connecting wires can be neglected. What is the total resistance in the circuit?

2. If the terminal voltage developed by the generator in question 1 is 110 V and the resistance of the generator is neglected, what current will flow through the circuit? Round your answer to two decimal places.

3. For the conditions described in questions 1 and 2, what will be the voltage drop in the device having a resistance of 8 ohms? Round your answer to one decimal place.

4. If the three electrical devices in question 1 are connected in parallel, as shown in the figure, what will be the total resistance of the group of devices? Round your answer to two decimal places.

5. Assume that the voltage developed by the generator in the circuit in question 4 is 110 V. If the resistance of the generator and the connecting wires is neglected, what current will flow through the wires between the generator and the group of three devices? Round your answer to one decimal place.

6. In the circuit in question 4, what portion of the total current will flow through the device that has a resistance of 8 ohms?

Answer 1

1)
`32 \Omega`

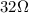
2) 3.44 A

3) 27.5 V

4)
`2.35\Omega`

5) 46.8 A

6) 13.7 A

Step-by-step explanation:

1)

Resistors are said to be connected in series if they are connected along the same branch. In this case, the total resistance of the circuit is equal to the sum of the individual resistances:

`R=R_1+R_2+...+R_n`

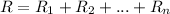
In this case, we have three resistances connected in series, so the total resistance of the circuit will be:

`R=R_1+R_2+R_3`

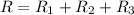
where:

`R_1=20\Omega` is the resistance of the 1st device

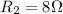`R_2=8 \Omega` is the resistance of the 2nd device

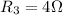`R_3=4\Omega` is the resistance of the 3rd device

Therefore, the total resistance is:

`R=20+8+4=32 \Omega`

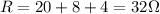
2)

Here we want to find the current in the circuit.

First of all, we are told that the resistance of the generator is neglected: this means that the total resistance of the circuit is that found in part 1).

Therefore, we can find the current using Ohm's Law:

`V=RI`

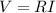
where

V is the terminal voltage of the battery

R is the total resistance of the circuit

I is the current in the circuit

In this problem, we have:

V = 110 V is the voltage of the battery

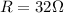`R=32\Omega` is the total resistance of the circuit

So the current is

`I=(V)/(R)=(110)/(32)=3.44 A`

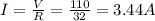
3)

The voltage drop across a certain resistor is given again by Ohm's Law:

`V_i = R_i I_i`

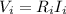
where

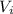`V_i` is the voltage drop across the resistor

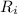`R_i` is the resistance of the resistor

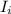`I_i` is the current through the resistor

In this problem:

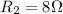`R_2=8 \Omega` is the resistor we are considering

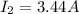`I_2=3.44 A` is the current through the resistor (in a series circuit, the current is the same for all devices in the circuit)

So, the voltage drop is

`V_2=I_2 R_2 =(3.44)(8)=27.5 V`

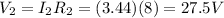
4)

Electrical devices are said to be connected in parallel if they are connected along different branches having same terminal points, so that they have same potential difference across them.

The total resistance for resistors in parallel is given by:

`(1)/(R)=(1)/(R_1)+(1)/(R_2)+....+(1)/(R_n)`

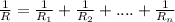
In this problem we have 3 resistors, so the total resistance is:

`(1)/(R)=(1)/(R_1)+(1)/(R_2)+(1)/(R_3)`

where

`R_1=20\Omega` is the resistance of the 1st device

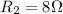`R_2=8 \Omega` is the resistance of the 2nd device

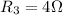`R_3=4\Omega` is the resistance of the 3rd device

Therefore, the total resistance is:

`(1)/(R)=(1)/(20)+(1)/(8)+(1)/(4)=0.425\\R=(1)/(0.425)=2.35\Omega`

5)

To find the total current in the circuit, we can use again Ohm's Law:

`V=RI`

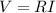
where:

V is the terminal voltage of the battery

R is the total resistance of the circuit

I is the current in the circuit

In this problem, we have:

V = 110 V is the voltage of the battery

`R=2.35\Omega` is the total resistance of the circuit

Therefore, solving for I, we find the current:

`I=(V)/(R)=(110)/(2.35)=46.8 A`

6)

The current across a certain resistor can be found using Ohm's Law, as before:

`V_i = R_i I_i`

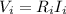
where:

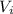`V_i` is the voltage drop across the resistor

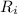`R_i` is the resistance of the resistor

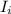`I_i` is the current through the resistor

In this problem:

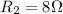`R_2=8 \Omega` is the resistor we are considering

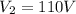`V_2=110 V` is the voltage drop across that resistor (in a parallel circuit, the voltage drop is the same across each resistor)

Solving for I, we find the current through it:

`I_2=(V_2)/(R_2)=(110)/(8)=13.7 A`