Question

.

What are the foci of the hyperbola whose equation is (y - 2)^2/64 - (x -4)^2/36 = 1?
(-6, 2) and (14, 2)
(-4, 2) and (12, 2)
(4,-8) and (4, 12)
(4,-6) and (4, 10)​

Answer 1

(C) (4,−8) and (4, 12)

Explanation:

took the test

Answer 2

(4,-8) and (4, 12)

Explanation:

The equation of the hyperbola given is:

`((y-2)^2)/(64)-((x-4)^2)/(36)=1`

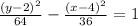
The general form of this hyperbola would be:

`(y^2)/(a^2)-(x^2)/(b^2)=1`

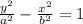
Thus, we can see that:

a^2 = 64

a = 8

and

b^2 = 36

b = 6

The distance from one focus to center is called "c", it goes by formula:

`c^2=a^2+b^2`

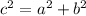
Let's find c:

`c^2=8^2 + 6 ^2\\c^2=100\\c=10`

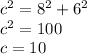
This is a vertical hyperbola and the center is found from the x and y's on the numerator:

(y-2)^2 means y = 2

(x-4)^2 = x = 4

Center is (4, 2)

We go 10 units vertically up, so from y = 2 , ten units up makes it y = 12

x = 4 and y = 12

(4,12)

We go 10 units vertically down, so from y =2, ten units down makes it y = -8

x = 4 and y = -8

(4, -8)

Foci coordinates:

(4,12) and (4,-8)