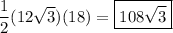Question

Find the area of the polygon

Answer 1

Looks like the larger triangle is equilateral (well, it must be, otherwise finding the area is impossible). That means the inradius is 6 and the outradius is 12, which is to say the altitudes (equal to the height, in this case) of this triangle have length 6 + 12 = 18.

In the smaller right triangle, the length of the missing leg is half the base of the larger triangle; call this length
`\frac b2` By the Pythagorean theorem,

`6^2+\left(\frac b2\right)^2=12^2\implies b=12\sqrt3`

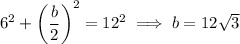
Then the area of the larger triangle is

`\frac12(12\sqrt3)(18)=\boxed{108\sqrt3}`