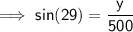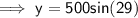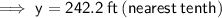Question

Find y.
Round to the nearest tenth:
290
500 ft
y
X
y = [ ? ]ft

Answer 1

y = 242.4 ft (nearest tenth)

Explanation:

Using the Alternate Interior Angle Theorem
the angle opposite side
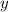`y` is 29°

Using the sine trig ratio:

`\sf sin(\theta)=(O)/(H)`

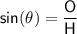
where:

• 
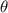  `\theta` is the angle
• O is the side opposite the angle
• H is the hypotenuse

Given:

• 
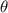  `\theta` = 29°
• O =
  `y`
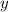
• H = 500 ft

Substitute given values and solve for y:

`\sf \implies sin(29)=(y)/(500)`

`\sf \implies y=500sin(29)`

`\sf \implies y=242.2\:ft\:(nearest\:tenth)`

Answer 2

• y = 242.4

• x = 437.3

First find the inner angle:

• 90° - 29°

• 61°

[ given hypotenuse = 500 ft ]

using sine rule:

`\sf sin(x)= (opposite)/(hypotensue)`

`\hookrightarrow \sf sin(61)= (x)/(500)`

`\hookrightarrow \sf x=sin(61)*500`

`\hookrightarrow \sf x=437.3`

using pythagoras theorem:

• a² + b² = c²

• y² + (437.3)² = 500²

• y = √58760.1

• y = 242.4