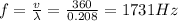Question

A student plucks a fixed-end string, creating a standing wave with 6.00 nodes (including any nodes at the ends). The string is tuned such that waves on the string travel 360m/s.

How many wavelengths are on the string?
What is the wavelength of the waves on the string?
What is the frequency of the waves on the string?

Answer 1

1) 2.5 wavelengths

2) 0.208 m

3) 1731 Hz

Step-by-step explanation:

1)

Standing waves are waves that do not propagate, but instead the particles of the medium just oscillate around a fixed position. Examples of standing waves are the waves produced on a string with fixed ends.

The points of a standing wave in which the amplitude of the oscillation is always zero are called nodes.

The two fixed ends of the string are two nodes. In this problem, we have a total of 6 nodes along the string: this means that there are 4 additional nodes apart from the two ends of the string.

Therefore, this also means that the string oscillate in 5 different segments.

One wavelength is equal to 2 segments of the oscillation: therefore, since here there are 5 segments, this means that the number of wavelengths that we have in this string is

`n=(5)/(2)=2.5`

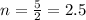
2)

The wavelength of a wave is the distance between two consecutive crests (or throughs) of the wave.

The wavelength of a standing wave can be also measured as the distance between the nth-node and the (n+2)-th node: so, basically, the wavelength in a standing wave is twice the distance between two nodes:

`\lambda = 2 d`

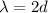
where

`\lambda` is the wavelength

d is the distance between two nodes

Here the length of the string is

L = 0.520 m

And since it oscillates in 5 segments, the distance between two nodes is

`d=(L)/(5)=(0.520)/(5)=0.104 m`

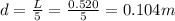
And therefore, the wavelength is

`\lambda=2d=2(0.104)=0.208 m`

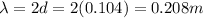
3)

The frequency of a wave is the number of complete oscillations of the wave per second.

The frequency of a wave is related to its speed and wavelength by the wave equation:

`v=f\lambda`

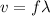
where

v is the speed

f is the frequency

`\lambda` is the wavelength

In this problem:

v = 360 m/s is the speed of the wave

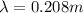`\lambda=0.208 m` is the wavelength

Therefore, the frequency is

`f=(v)/(\lambda)=(360)/(0.208)=1731 Hz`