Answer:
The length of the radius of the circle is 7 mm
Explanation:
see the attached figure to better understand the problem
we know that
If HK is tangent to circle O at point K
then
The radius OK is perpendicular to segment HK and triangle OKH is a right triangle
Applying the Pythagorean Theorem
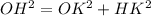
we have
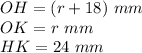
substitute
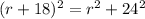
solve for r
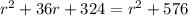

therefore
The length of the radius of the circle is 7 mm