Answer:
Price elasticity of demand is 1.133
Step-by-step explanation:
Step-by-step explanation:
Given Data;
q = (94 − p)^2
p = price per case of tissue
q = demand in weekly sales
p = $34
Price elasticity of demand E =?
To calculate the price elasticity of demand, we use the formula;
E =⁻
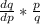 ----------------------1
----------------------1
By differentiating q with respect to p, we have
dp/dq = (94 − p)^2
=2( 94-p) * (-1)
= -2(94-p)
Substituting into equation 1,
where dp/dq = -(94-p) and q = (94 − p)^2
E =( -) -2(94-p) * p/((94 − 34)^2)
When the price is at $34, Elasticity becomes
E = -2(94-34) * 34/((94 − 34)^2)
=( 2*60) * (34/60²)
=120 * 34/3600
= 120 * 0.00944
=1.133