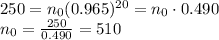Answer:
510 gorillas
Explanation:
In this problem, the population of gorillas is decreasing at a rate of 3.5 % per year.
We can write an expression for the population of gorillas as follows:
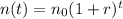
where
n(t) is the number of gorillas after t years
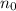 is the number of gorillas at t = 0
is the number of gorillas at t = 0
r is the grow rate of the population
t is the number of years
Here we have:
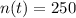 is the number of gorillas when t = 20 years
is the number of gorillas when t = 20 years
 is the grow rate of the population
is the grow rate of the population
So the equation becomes:
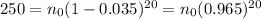
And solving for
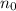 , we find the initial number of gorillas:
, we find the initial number of gorillas: