Question

A gas station sells two grades of gasoline: regular and super. These are priced at $2.00 and $3.00 per gallon, respectively. Let X₁ and X₂ denote the amounts of these grades purchased (gallons) on a particular day. Suppose X₁ and X₂ are independent Normal random variables with E(X₁) = 1000, sd(X₁) = 90, E(X₂) = 800, and sd(X₂) = 45. The revenue from sales is Y = 2X₁ + 3X₂. (a) Find the mean and standard deviation of Y, i.e., E(Y) and sd(Y). (b) Find the probability that the revenue Y does not exceed 4500. Hint: Y is Normally distributed. (c) Find the probability that the gas station sells regular gasoline more, i.e., pr (X₁ > X₂). Attach the R codes or write out the formula(s) you used for full credit.

Answer 1

(a) E (Y) = 440, SD (Y) = 225

(b) P = 0.6716

(c) P = 0.9766

Explanation:

Detailed explanation is given in the attached document.

Answer 2

(a) E(Y) = 4400

sd (Y) =225

(b) P(Y ≤ 4500) = 0.67003

(c) P (X₁ > X₂) = 0.31744

Explanation:

(a) Here we have

Y = 2·X₁ + 3·X₂

Therefore E(Y) = 2·E(X₁) + 3·E(X₂) = 2000 + 2400 = 4400

sd(Y) is given by

Variance Y = (sd (Y))² = 2²·(sd (X₁))² + 3²·(sd (X₂))²

= 4·8100 + 9·2025 = 50625

sd (Y) = √50625 = 225

(b) The probability that the revenue does not exceed 4500 is given by

P(Y ≤ 4500) = P(z ≤0.444)

z =
`\frac{\overline{\rm x} - \mu} {\sigma /√(n) }`

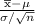
z =
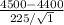`\frac{4500 - 4400} {225 /√(1) }` = 0.444

Therefore from the normal distribution table, we have

P = 0.67003

(c) The probability that the P(X₁ > X₂)

Since the gas station sells 2 portions of X₁ to 3 portions of X₂

Therefore, the probability that the gas station sells more of X₁ is given by

₅C₀ × 2/5⁰×3/5⁵ = 0.07776

₅C₁ × 2/5¹×3/5⁴= 0.2592

₅C₂ × 2/5²×3/5³ = 0.3456

P (X₁ > X₂) = 1 - 0.68256 = 0.31744