We know sum of interior angles in any triangle is 180°. Your specific triangle is a right triangle (one angle must be 90°) and we are also given another angle (57°) that means we can find angle T,
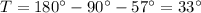
Use the sine function to find
 ,
,
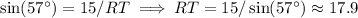
Use the tangent function to find
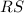 ,
,
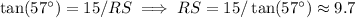
Hope this helps.