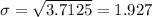Question

Assume the student body of a large university (with over 10,000 students) is 55% female, 45% male. Fifteen students are selected randomly. Let X represent the number of females in the sample. (4 pts) Find the mean, variance, and standard deviation of X.

Answer 1

Mean = 8.25

Variance = 3.7125

Standard deviation = 1.927

Explanation:

Let the probability of X be p.

Then
`p=55\% = 0.55`

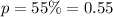
It follows that X is a binomial random variable.

For a binomial distribution, for n samples,

Mean,
`\mu = np`

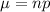
Variance,
`\sigma^2 = np(1-p)`

Standard deviation,
`\sigma =√(np(1-p))`

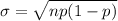
Using values in the question, n = 15

Mean =
`\mu = 15*0.55 = 8.25`

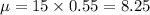
Variance =
`\sigma^2 = 15*0.55*(1-0.55) = 15*0.55*0.45 = 3.7125`

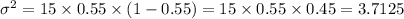
Standard deviation =
`\sigma =√(3.7125) = 1.927`