Answer:
The probability that the proportion of the core being used at any particular time will be less than 0.10 is 0.08146
Explanation:
 1/3 0.33 = 33.33 %
1/3 0.33 = 33.33 %
The Probability of that the proportion of the core being used at any particular time will be less than 0.10 is given by
PDF =
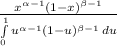
where x = 0.1
α = 2 and β = 4
PDF =
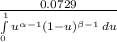 = 1.458
= 1.458
CDF =
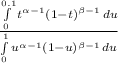 = 0.08146
= 0.08146
The probability that the proportion of the core being used at any particular time will be less than 0.10 = 0.08146.