Question

A random sample of 8 fields of barley has a mean yield of 49.6 bushels per acre and standard deviation of 2.33 bushels per acre. Determine the 99% confidence interval for the true mean yield. Assume the population is approximately normal. Step 1 of 2 : Find the critical value that should be used in constructing the confidence interval. Round your answer to three decimal places.

Answer 1

99% confidence interval for the true mean yield is [46.718 , 52.482].

Explanation:

We are given that a random sample of 8 fields of barley has a mean yield of 49.6 bushels per acre and standard deviation of 2.33 bushels per acre.

Firstly, the pivotal quantity for 99% confidence interval for the true mean yield is given by;

P.Q. =
`(\bar X - \mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

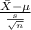where,
`\bar X` = sample mean yield = 49.6 bushels per acre

s = sample standard deviation = 2.33 bushels per acre

n = sample of fields of barley = 8

`\mu` = true population mean

Here for constructing 99% confidence interval we have used t statistics because we don't know about population standard deviation.

So, 99% confidence interval for the true mean,
`\mu` is ;

P(-3.499 <
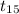`t_1_5` < 3.499) = 0.99 {As the critical value of t at 7 degree of

freedom are -3.499 & 3.499 with P = 0.5%}

P(-3.499 <
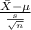`(\bar X - \mu)/((s)/(√(n) ) )` < 3.499) = 0.99

P(
`-3.499 * {(s)/(√(n) ) }` <
`{\bar X - \mu}` <
`3.499 * {(s)/(√(n) ) }` ) = 0.99

P(
`\bar X -3.499 * {(s)/(√(n) )` <
`\mu` <
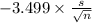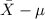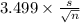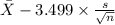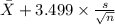`\bar X +3.499 * {(s)/(√(n) )` ) = 0.99

99% confidence interval for
`\mu` = [
`\bar X -3.499 * {(s)/(√(n) )` ,
`\bar X +3.499 * {(s)/(√(n) )` ]

= [
`49.6 -3.499 * {(2.33)/(√(8) )` ,
`49.6 +3.499 * {(2.33)/(√(8) )` ]

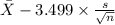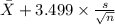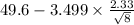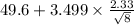= [46.718 , 52.482]

Therefore, 99% confidence interval for the true mean yield is [46.718 , 52.482].