Question

In Haiti, public transportation is often by taptaps, small pickup trucks with seats along the sides of the pickup bed and railings to which passengers can hang on. Typically they carry two dozen or more passengers plus an assortment of chickens, goats, luggage, etc. Putting this much into the back of a pickup truck puts quite a large load on the truck springs.

A truck has springs for each wheel, but for simplicity assume that the individual springs can be treated as one spring with a spring constant that includes the effect of all the springs. Also for simplicity, assume that all four springs compress equally when weight is added to the truck and that the equilibrium length of the springs is the length they have when they support the load of an empty truck.
Part A
A 60-kg driver gets into an empty taptap to start the day's work. The springs compress 0.02 m. What is the effective spring constant of the spring system in the taptap?
Enter the spring constant numerically in newtons per meter. Express your answer using two significant figures.
k =2.9×10^4 N/m
Part B
After driving a portion of the route, the taptap is fully loaded with a total of 25 people with an average mass of 60 kg per person. In addition, there are three 15 kg goats, five 3- kg chickens, and a total of 25 kg of bananas on their way to the market. Assume that the springs have somehow not yet compressed to their maximum amount. How much are the springs compressed?

Answer 1

A. k=29400N/m

B. x=0.528m

Step-by-step explanation:

Part A.

The net force exerted by the driver on the springs is equal to his weight. Assuming the springs reach an equilibrium, we have that this force is equal and opposite in direction to the force exerted by the springs. So, from the equation of the force exerted by a spring, we have:

`F=-kx\\\\mg=kx\\\\\implies k=(mg)/(x)`

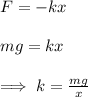
Plugging in the given values for the mass of the driver and the compression lenght, we obtain:

`k=((60kg)(9.8m/s^(2)))/(0.02m)=29400N/m`

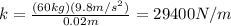
So, the spring constant of the spring system in the taptap is 29400N/m.

Part B.

We can use the same relationship as in the part A, in this case solving for x:

`x=(mg)/(k)`

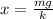
In "m", we have to put the total mass that is in the taptap, so we sum the information given:

`m=25(60kg)+3(15kg)+5(3kg)+25kg=1585kg`

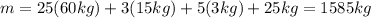
Finally, we calculate x using this value for m:

`x=((1585kg)(9.8m/s^(2)))/(29400N/m)\\ \\x=0.528m`

Then, the springs are compressed 0.528m.