Answer:
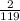
Explanation:
We have been given that Trevor has a bag of jelly beans. There are 10 red, 15 green, 5 orange, and 5 purple jelly beans in the bag.
The probability of choosing an orange jelly will be total number of orange jellies over all jellies.
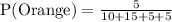
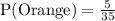
Now, he again chooses an orange jelly and eats it. Since he already ate 1 orange jelly, so orange jelly left is 4 and total jellies would be 34.
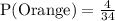
Using multiplication rule of probability, we will get:
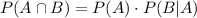
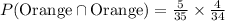

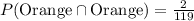
Therefore, the probability that Trevor randomly chooses 1 orange jellybean, eats it, and then chooses another orange jellybean and eats it would be
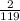 .
.