Answer:
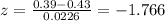
And we can find this probability using the complement rule and the normal standard table or excel and we got:

Explanation:
For this case we can define the population proportion p as "true proportion of surgeons" and we can check if we can use the normal approximation for the distribution of

1)
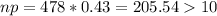
2)
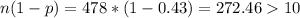
3) Random sample: We assume that the data comes from a random sample
Since we can use the normal approximation the distribution for
 is given by:
is given by:
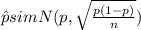
With the following parameters:

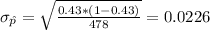
And we want to find this probability:
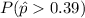
And we can use the z score formula given by:
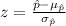
And if we calculate the z score for
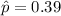 we got:
we got:
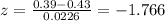
And we can find this probability using the complement rule and the normal standard table or excel and we got:
