Answer:
445.9 m
Step-by-step explanation:
The law of conservation posits that the total momentum of two objects prior to collision is equal to the total momentum of the two objects after the collision has occurred.
i.e
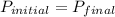
where;
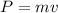
m = mass of the object
v = velocity of the object
here, the initial momentum
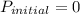
The final momentum
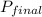 = sum of the momentum of heavier fragment and lighter fragment.
= sum of the momentum of heavier fragment and lighter fragment.
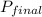 =
=
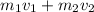 ----- expression (1)
----- expression (1)
where
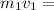 the mass and the velocity of the lighter fragment
the mass and the velocity of the lighter fragment
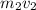 = the mass and the velocity of the heavier fragment
= the mass and the velocity of the heavier fragment
From the question; we can say:
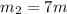 (i.e the one that is seven times as massive as the other)
(i.e the one that is seven times as massive as the other)
we write the above expression (1) as:

Since:
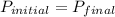
0 =
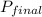
0 =
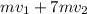
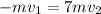

Let's determine the kinetic energy and the work done by the frictional force in both fragments
To start with the lighter fragment; the kinetic energy is expressed as;

where;
m = mass
v = v₁ = velocity
 = change in direction
= change in direction
So;
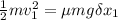
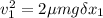 --------- equation (1)
--------- equation (1)
For the heavier fragment ;
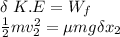
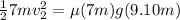
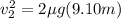 ------------ equation (2)
------------ equation (2)
Equating equation (1) by equation (2); we have:
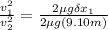
Replacing
 ; from the above relation of the velocities; we have
; from the above relation of the velocities; we have
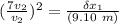

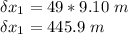
∴ The lighter fragment slide 445.9 m far from the initial point of explosion.