Question

(4) A spherical balloon is being inflated so that its diameter is increasing at a constant rate of 6 cm/min. How quickly is the volume of the balloon increasing when the diameter is 50 cm

Answer 1

In terms of its radius
`r`, the volume of the balloon is

`V(r)=\frac{4\pi}3r^3`

The diameter
`d` is twice the radius, so that in terms of its diameters, the balloon's volume is given by

`V(d)=\frac{4\pi}3\left(\frac d2\right)^3=\frac\pi6d^3`

Differentiate both sides with respect to time
`t`:

`(\mathrm dV)/(\mathrm dt)=\frac\pi2d^2(\mathrm dd)/(\mathrm dt)`

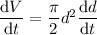
The diameter increases at a rate of
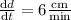`(\mathrm dd)/(\mathrm dt)=6(\rm cm)/(\rm min)`. When the diameter is
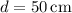`d=50\,\mathrm{cm}`, we have

`(\mathrm dV)/(\mathrm dt)=\frac\pi2(50\,\mathrm{cm})^2\left(6(\rm cm)/(\rm min)\right)=7500\pi\frac{\mathrm{cm}^3}{\rm min}`

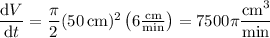
or about 23,562 cc/min (where cc = cubic centimeters)