Question

As a store manger you would like to find out the average time it takes to unload the truck which delivers the merchandise for your store. For this purpose, you have taken a random sample of 35 days and found the average unload time to be 204 minutes for the sample. You also found that the standard deviation is 30 minutes for the sample. Find the upper boundary of the 95% confidence interval for the average unload time. Round the answer to two decimal places.

Answer 1

The upper boundary of the 95% confidence interval for the average unload time is 214.30 minutes.

Explanation:

We are given that a store manger you would like to find out the average time it takes to unload the truck which delivers the merchandise for your store.

For this purpose, you have taken a random sample of 35 days and found the average unload time to be 204 minutes for the sample. You also found that the standard deviation is 30 minutes for the sample.

Assuming the population has a normal distribution.

Firstly, the pivotal quantity for 95% confidence interval for the average unload time is given by;

P.Q. =
`(\bar X - \mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

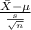where,
`\bar X` = sample average unload time = 204 minutes

s = sample standard deviation = 30 minutes

n = sample of days = 35

`\mu` = population average unload time

Here for constructing 95% confidence interval we have used t statistics because we don't know about population standard deviation.

So, 95% confidence interval for the population​ mean,
`\mu` is ;

P(-2.032 <
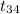`t_3_4` < 2.032) = 0.95 {As the critical value of t at 34 degree of

freedom are -2.032 & 2.032 with P = 2.5%}

P(-2.032 <
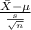`(\bar X - \mu)/((s)/(√(n) ) )` < 2.032) = 0.95

P(
`-2.032 * {(s)/(√(n) ) }` <
`{\bar X - \mu}` <
`2.032 * {(s)/(√(n) ) }` ) = 0.95

P(
`\bar X-2.032 * {(s)/(√(n) ) }` <
`\mu` <
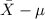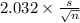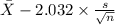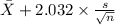`\bar X+2.032 * {(s)/(√(n) ) }` ) = 0.95

95% confidence interval for
`\mu` = [
`\bar X-2.032 * {(s)/(√(n) ) }` ,
`\bar X+2.032 * {(s)/(√(n) ) }` ]

= [
`204-2.032 * {(30)/(√(35) ) }` ,
`204+2.032 * {(30)/(√(35) ) }` ]

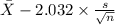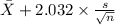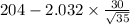= [193.69 , 214.30]

Hence, 95% confidence interval for the average unload time is [193.69 , 214.30].

So, the upper boundary of the 95% confidence interval for the average unload time is 214.30 minutes.

Answer 2

The upper boundary of the 95% confidence interval for the average unload time is 264.97 minutes

Explanation:

We have the standard deviation for the sample, but not for the population, so we use the students t-distribution to solve this question.

The first step to solve this problem is finding how many degrees of freedom, we have. This is the sample size subtracted by 1. So

df = 35 - 1 = 35

95% confidence interval

Now, we have to find a value of T, which is found looking at the t table, with 34 degrees of freedom(y-axis) and a confidence level of
`1 - (1 - 0.9)/(2) = 0.975([tex]t_(975)`). So we have T = 2.0322

The margin of error is:

M = T*s = 2.0322*30 = 60.97

The upper end of the interval is the sample mean added to M. So it is 204 + 60.97 = 264.97

The upper boundary of the 95% confidence interval for the average unload time is 264.97 minutes