Question

A 4 meter tall bear is walking in the woods and sees honey flavoured chips strapped to a flashlight hanging from a tree 7 meters above the ground. The bear, smelling honey, decides to raid the chips package and starts walking towards the honey at 6 meters per second. As the bear walks, the flashlight is casting a shadow behind the bear which gets shorter and shorter. (1) When the bear is 5 meters away from the honey, how fast is the length of his shadow decreasing? (Assume that the honey chips and the flashlight are at exactly the same point.)

Answer 1

The length of the shadow is decreasing 8 metres per second.

Explanation:

In the attached figure, we draw the situation of the bear approaching the tree.

We can use the Tales to make some calculations.

The proportion between the height of the bear (h) and his shadow (S) is equal to the proportion between the height of the flashlight (H) and the sum of the distance of the bear (d) and the bear shadow.

This can be written as:

`(h)/(S) =(H)/(S+d)`

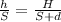
If we clear S we have:

`S*H=S*h+d*h\\\\(H-h)*S=d*h\\\\S=((h)/(H-h)) d`

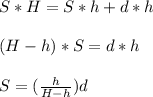
We know that the distance is a function of time and it is reduced, as the bear approaches the tree, as a rate of 6 m/s.

We can express then the rate of variation of the shadow S as:

`\Delta S=S_2-S_1=((h)/(H-h)) (d_2-d_1)=((h)/(H-h)) \Delta d\\\\\\\Delta d=-6\\\\H=7\\\\h=4\\\\\\\Delta S=((4)/(7-4)) *(-6)=(4)/(3) *(-6)=-8`

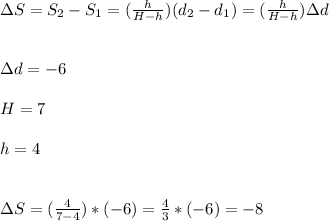
The length of the shadow is decreasing 8 metres per second.