Question

Suppose that NBA players average 33 points per game with a standard deviation of 7.46. A random sample of 110 players is taken. What is the probability that the sample mean is greater than 32.6?

Answer 1

Probability that the sample mean is greater than 32.6 is 0.7123.

Explanation:

We are given that NBA players average 33 points per game with a standard deviation of 7.46.

A random sample of 110 players is taken. Also, assuming data follow normal distribution.

Let
`\bar X` = sample mean

The z-score probability distribution for sample mean is given by;

Z =
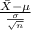`\frac{ \bar X -\mu}{{(\sigma)/(√(n) ) }} }` ~ N(0,1)

where,
`\mu` = average points per game = 33

`\sigma` = standard deviation = 7.46

n = sample of players = 110

The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.

So, probability that the sample mean is greater than 32.6 is given by = P(
`\bar X` > 32.6)

P(
`\bar X` > 32.6) = P(
`\frac{ \bar X -\mu}{{(\sigma)/(√(n) ) }} }` >
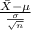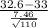`\frac{ 32.6-33}{{(7.46)/(√(110) ) }} }` ) = P(Z > -0.56) = P(Z < 0.56) = 0.7123

Now, in the z table the P(Z > -x) is same as P(Z < x). So, the above probability is calculated by looking at the value of x = 0.56 in the z table which has an area of 0.7123.

Therefore, probability that the sample mean is greater than 32.6 is 0.7123.

Answer 2

0.7131 is the probability that the sample mean is greater than 32.6

Explanation:

We are given the following information in the question:

Mean, μ = 33

Standard Deviation, σ = 7.46

Sample size, n = 110

Standard error due to sampling =

`=(\sigma)/(√(n)) = (7.46)/(√(110)) = 0.7112`

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

P(sample mean is greater than 32.6)

`P( x > 32.6) = P( z > \displaystyle(32.6 - 33)/(0.7112)) = P(z > -0.5624)`

`= 1 - P(z \leq -0.5624)`

Calculation the value from standard normal z table, we have,

`P(x > 32.6) = 1 - 0.2869 = 0.7131`

0.7131 is the probability that the sample mean is greater than 32.6.