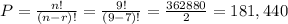Answer:
1) If the order doesn't matter, there are 36 possible outcomes.
2) If the order does matter, there are 181,440 possible outcomes.
Explanation:
1) In the case when the order doesn't matter , we have to calculate a combination of 7 screws in 9 holes.
We use the formula for combinations:
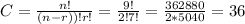
being r: the number of screws and n: the number of holes.
2) When the order does matter, the possible outcomes are called permutations. We have permutations of 7 screws in 9 holes.
We use the formula for permutations: