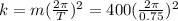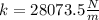Answer:
The spring constant for a single spring is 28073.5 N/m
Step-by-step explanation:
First if we assume the vibration of the approximates simple harmonic motion, the to each of the springs we can associate a natural frequency of vibration that is defined for a simple spring as:
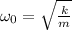 (1)
(1)
with k the spring constant and m the mass attached to the spring
Natural frequency is related with the period (T) of the oscillation as follows:
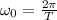 (2)
(2)
We can equate (1) and (2):
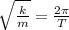
solving for k:
 (3)
(3)
k is the spring constant for a single spring, if we assume the weight of the car and the people is uniformly distributed on the four springs, then the mass m is:
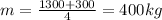
Now we have all the values to put on (3):