Question

A​ person's blood pressure is monitored by taking 4 readings daily. The probability distribution of his reading had a mean of 133 and a standard deviation of 5. a. Each observation behaves as a random sample. Find the mean and the standard deviation of the sampling distribution of the sample mean for the four observations each day. b. Suppose that the probability distribution of his blood pressure reading is normal. What is the shape of the sampling​ distribution? c. Refer to​ (b). Find the probability that the sample mean exceeds 140.

Answer 1

a) Mean = 133, Standard deviation = 2.5

b) Normal distribution

c) 0.0026

Explanation:

We are given the following in the question:

Sample size, n = 4

Mean = 133

Standard deviation = 5

a) Mean and the standard deviation of the sampling distribution of the sample mean for the four observations each day.

The sampling distribution has a mean equal to the population mean

`\bar{x} = \mu = 133`

The standard deviation of the sampling distribution is given by:

`\sigma_s = (\sigma)/(√(n)) = (5)/(√(4)) = 2.5`

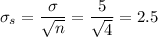
b) Shape of the sampling​ distribution

Central limit theorem:

When a large sample is drawn from a normal distribution, then the distribution of sample means approaches a normal distribution.

Since the distribution is normal, the sampling distribution of the sample mean will be bell shaped and follow a normal distribution.

c) P(sample mean exceeds 140)

`P( x > 140) = P( z > \displaystyle(140 - 133)/(2.5)) = P(z > 2.8)`

`= 1 - P(z \leq 2.8)`

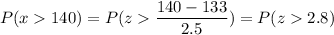
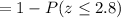
Calculation the value from standard normal z table, we have,

`P(x > 140) = 1 - 0.9974 = 0.0026`

0.0026 is the probability that the sample mean exceeds 140.