Question

A fast food restaurant executive wishes to know how many fast food meals adults eat each week. They want to construct a 85% confidence interval with an error of no more than 0.08. A consultant has informed them that a previous study found the mean to be 5.6 fast food meals per week and found the standard deviation to be 1.3. What is the minimum sample size required to create the specified confidence interval? Round your answer up to the next integer.

Answer 1

The sample size must be 548 to have a margin of error of no more than 0.08.

Explanation:

We are given the following in the question:

Sample mean = 5.6

Standard deviation = 1.3

Significance level = 15%

Margin of error = 0.08

We have to estimate the sample size.

Margin of error =

`z_(critical)(\sigma)/(√(n))`

`z_(critical)\text{ at}~\alpha_(0.15) = 1.44`

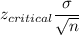
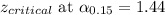
Putting values, we get

`0.08 = 1.44* (1.3)/(√(n))\\\\√(n) = 1.44(* 1.3)/(0.08)\\\\√(n) = 23.4\\n =547.56\approx 548`

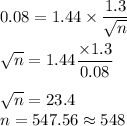
Thus, the sample size must be 548 to have a margin of error of no more than 0.08.