Answer:
![x(t) = (6\,m)\cdot \cos \left[\left(2\,(rad)/(s) \right)\cdot t-0.5\pi \right]](https://img.qammunity.org/2021/formulas/physics/college/yq7ya697ulhd4lvvua3j821412n564xhms.png)
Step-by-step explanation:
This problem describes a system experimenting a simple harmonic motion. The spring constant is determined by the Hooke's Law:
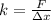
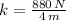
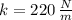
The angular frequency is:
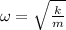
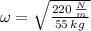
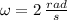
The position and velocity functions for the motion of the mass-spring system is:
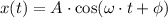
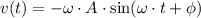
The initial condition for the system are:
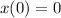 ,
,
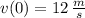
Equation at initial time are:
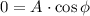
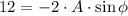
By dividing the first equation by the second one:
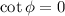
Which corresponds to

The amplitude is:
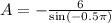
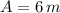
The equation of motion is:
![x(t) = (6\,m)\cdot \cos \left[\left(2\,(rad)/(s) \right)\cdot t-0.5\pi \right]](https://img.qammunity.org/2021/formulas/physics/college/yq7ya697ulhd4lvvua3j821412n564xhms.png)