Question

A right triangle contains a 38° angle whose adjacent side measures 10 centimeters. What is the length of the hypotenuse, to the nearest hundredth of a centimeter

Answer 1

12.69 inches.

Explanation:

Let h represent the length of the hypotenuse.

We have been given that a right triangle contains a 38° angle whose adjacent side measures 10 centimeters. We are asked to find the length of the hypotenuse.

We know that cosine relates adjacent side to hypotenuse of right triangle.

`\text{cos}=\frac{\text{Adjacent}}{\text{Hypotenuse}}`

`\text{cos}(38^(\circ))=(10)/(h)`

`h=\frac{10}{\text{cos}(38^(\circ))}`

`h=(10)/(0.788010753607)`

`h=12.690182`

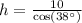
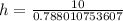
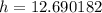
Upon rounding to the nearest hundredth of a centimeter, we will get:

`h\approx 12.69`

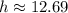
Therefore, the length of the hypotenuse is approximately 12.69 inches.