Question

A customer at Marty’s Fruit Stand picks a sample of 3 oranges at random from a crate containing 60 oranges, of which 4 are rotten. In how many ways can you chose at least two rotten oranges?

Answer 1

340 ways

Explanation:

Given:

Total number of oranges = 60

Number of rotten oranges = 4

Number of oranges picked = 3

Now, number of good oranges = Total number - Rotten oranges

= 60 - 4 = 56

Now, we need to pick at least two rotten oranges.

So, the possible outcomes can be as follows:

1. 2 rotten oranges + 1 good orange = 3 oranges
2. 3 rotten oranges + 0 good orange = 3 oranges

Now, number of ways of picking 'r' distinct objects from a total of 'n' objects is given as:

`^nCr=(n!)/(r!(n-r)!)`

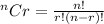
Now, picking 2 rotten oranges from a total of 4 rotten oranges is:

`^4C_2=(4!)/(2!2!)=(4* 3* 2)/(4)=6`

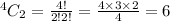
Similarly, picking 3 rotten oranges from a total of 4 rotten oranges is:

`^4C_3 =(4!)/(3!*1!)=(4* 3!)/(3!)=4`

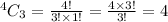
Now, picking 1 good orange from a total of 56 good oranges is:

`^(56)C_1=56`

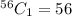
Picking 0 good oranges means picking no good oranges.

Therefore, the total number of ways of picking at least 2 rotten oranges is the sum of the above two possibilities and is given as:

At least 2 rotten out of 3 picked = (2 rotten and 1 good) or 3 rotten

= 6 × 56 + 4

= 336 + 4 = 340 ways

Therefore, there are 340 ways of picking at least 2 rotten oranges when 3 oranges are picked from a total of 60 oranges.