Question

A 1.94-m-diameter lead sphere has a mass of 5681 kg. A dust particle rests on the surface. What is the ratio of the gravitational force of the sphere on the dust particle to the gravitational force of the earth on the dust particle?

Answer 1

To develop this problem we will apply Newton's laws regarding gravitational forces, both in space and on earth. From finding this relationship, leaving the variable of the dust mass open, we will find the relationship of the forces between the two surfaces. Our values are,

`\text{Diameter of the lead sphere} = D=1.940m`

`\text{Mass of the lead sphere} = m_1 = 5681kg`

`\text{Mass of the dust particle} = m_2`

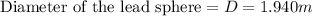
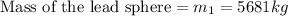
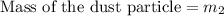
Distance between the center of lead sphere to dust particle

`r = (D)/(2)`

`r = (1.940m)/(2)`

`r = 0.97m`

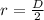
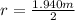
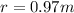
Gravitational force of the sphere on the dust particle:

`F = (Gm_1m_2)/(r^2)`

`F = ((6.67*10^(-11)N\cdot m^2/kg^2)(5681kg)(m_2))/((0.97m)^2)`

`F = (4.027*10^(-7) N/kg)m_2`

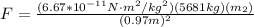
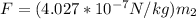
Weight of the dust particle

`W = m_2 g`

`W = m_2 (9.8m/s^2)`

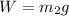
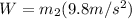
Ratio of F and W:

`(F)/(W) = ((4.07*10^(-7)N/kg) m_2))/(m_2(9.8m/s^2))`

`(F)/(W) = 4.153*10^(-8)`

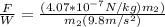
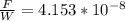
Therefore the ratio is
`4.153*10^(-8)`