Question

An electron passes through a point 2.35 cm 2.35 cm from a long straight wire as it moves at 32.5 % 32.5% of the speed of light perpendicularly toward the wire. At that moment a switch is flipped, causing a current of 18.9 A 18.9 A to flow in the wire. Find the magnitude of the electron's acceleration a a at that moment.

Answer 1

a = 2.8 × 10¹⁵m/s²

Step-by-step explanation:

The expression of magnetic field is

`F=qv\ * B\\B=(\mu_0I)/(2\pi r)`

`\mu` is the permitivity space

`I` is the current in wire

r is the distance from the wire

substitute

`\mu=4\pi*10^(-7)T.m/a`

I = 18.9A

r = 2.35cm

`B=(\mu_0I)/(2\pi r)`

`B = ((4\pi *10^-^7)(18.9))/(2\pi (2.35*10^-^2)) \\\\B = 1.6435*10^-^4T`

The direction of the magnetic field is perpendicular to the direction of the motion of the electron. Thus

The magnetic force exerted on electrons passing through a straight conducting wire is

`F=qvB`

`=(1.6*10^(-19)C)(9.75*10^(7)m/s)(1.6435*10^(-4)T)\\\\=2.56*10^(-15)N`

And by replacing this factor in

F=ma we have

`a=(F)/(m)`

`=(2.564*10^(-15)N)/(9.11*10^(-31)kg)\\\\=2.8*10^(15)(m)/(s^2)`

Answer 2

a = 2.75*10^{15}m/s^2

Step-by-step explanation:

The acceleration of the electron is generated by the Lorenz's force, due to the magnetic field produced by the wire. Hence, we have

`F=qv\ * B\\B=(\mu_0I)/(2\pi r)`

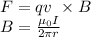
I=18.9 A

r=2.35cm=0.0235m

mu=4pi*10^{-7}

v=(0.325)(3*10^{8}m/s)=9.75*10^{7}m/s

q=1.6*10^{-19} C

By replacing these values in the expression for B we have

B=1.6*10^{-4} T

The direction of the magnetic field is perpendicular to the direction of the motion of the electron. Thus

`F=qvB=(1.6*10^(-19)C)(9.75*10^(7)m/s)(1.6*10^(-4)T)=2.15*10^(-15)N`

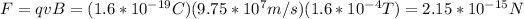
And by replacing this factor in F=ma we have

`a=(F)/(m)=(2.5*10^(-15)N)/(9.1*10^(-31)kg)=2.75*10^(15)(m)/(s^2)`

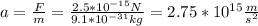
where we have used the mass of the electron.

hope this helps!!