Question

The chair's mass is 18.8 kg. The force you exert on the chair is 160 N directed 26 degrees below the horizontal. While you slide the chair a distance of 6.20 m , the chair's speed changes from 1.50 m/s to 2.90 m/s . Find the work done by friction on the chair

Answer 1

To solve this problem it is necessary to apply the concepts related to energy conservation. Therefore, the work done will initially be equivalent to the change in kinematic energy. And this kinematic energy will be equivalent to the sum of energy (work) carried out by force and friction. In this way we have to

`E = (1)/(2) m (v_f^2-v_i^2)`

`E = (1)/(2) (18.8kg)((2.9m/s)^2-(1.5m/s)^2)`

`E = 57.904J`

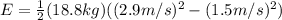
Now,

`E = \Delta W`

`E = W_(Force)+W_(Friction)`

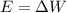
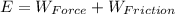
For each one we have

`W_(Force) = F dcos(\theta)`

`W_(Force) = (160)(6.20*cos(26))`

`W_(Force) = 891.604J`

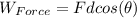
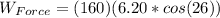
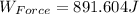
Then at the equation of equilibrium of energy we have,

`57.904J = 891.604J+W_(Friction)`

`W_(Friction) = 57.904-891.604`

`W_(Friction) = -833.7J`

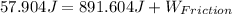
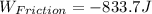
Therefore the work done by friction on the chair is -833.7J