Answer:
Therefore the number of product is 11.42 to minimize the average cost .
Explanation:
Given that,
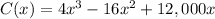
where C(x) is cost of manufacturing of x items.
Differentiating with respect to x

Again differentiating with respect to x
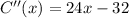
To find the minimum cost, we set C'(x)=0
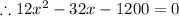
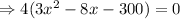
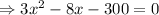 [ since 4≠0]
[ since 4≠0]
Applying quadratic formula
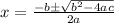 , here a= 3, b= -8, c=-300
, here a= 3, b= -8, c=-300

=11.42, -8.76
The number of item is negative, it can't make sense.
∴x=11.42
Now
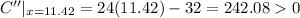
Therefore when x= 11.42, the cost of manufacturing will minimum.
Therefore the number of product is 11.42 to minimize the average cost .