Question

(25 pts) Consider a random variable X with density function f X (x) = x , 0 ≤ x ≤1 0, else ⎧ ⎨ ⎪ ⎩ ⎪ . a. (3) Carefully sketch by hand the density function f X (x) . Be sure to dimension both axes. b. (4) Find the mean and variance of X . c. (4) Suppose we generate a new random variable Y = Q(X) by quantizing X according to the following 3-level uniform quantizer: Q(x) = − 2 3 , −1≤ x < − 1 3 0, − 1 3 ≤ x < 1 3 2 3 , 1 3 ≤ x ≤1

Answer 1

Explanation:

It seems that this question is incomplete, and unfortunately, no reference was found in the internet. However, it seems that question is about calculating the variance and the mean of a random variable, based on its pdf (probability density funtion). Recall that a function must fulfill the following property for it to be a pdf

`\int_(-\infty)^(\infty) f(x) dx =1`

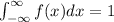
Also, recall that the following formulas

`\text{E}\[X\] = \int_(-\infty)^(\infty) xf(x) dx` (the mean)

`\text{Var}\[X\] = \int_(-\infty)^(\infty) x^2f(x) dx-(\text{E}\[X\])^2`.

Let us illustrate this calculations with an example.

Consider the function f(x) = 2x if
`0\leq x \leq 1` and 0 otherwise. By easy calculations, we can check that f(x) is indeed a pdf (it integrates up to 1). Hence it's mean is

`\text{E}\[X\] = \int_(0)^(1) x\cdot2x dx = \left.(2)/(3)x^3\rigth|_(0)^1 = (2)/(3)`

and the variance is given by

`\text{Var}\[X\] = \int_(0)^(1) x^2\cdot 2x dx -((2)/(3))^2= \left.(1)/(2)x^4\right|_(0)^1-((2)/(3))^2 = (1)/(2)-(4)/(9)= (1)/(18)`