Question

The mean score on a particular standardized test is 500, with a standard deviation of 100. To assess whether a training course has been effective in improving scores on the test, we take a random sample of 100 students from the course and find that the average score of this sample is 550. Which function would correctly calculate the 95% range of likely sample means under the null hypothesis?

Answer 1

The 95% confidence intervals are (530.4 ,569.6) of sample means under the null hypothesis

Explanation:

The mean score on a particular standardized test is μ=500

and also standard deviation of(σ) = 100.

random sample n =100

mean of the sample from data Χ⁻=550

95% of confidence intervals

The mean score on a particular standardized test is 'μ"

and also standard deviation of( σ) the population

size of the sample 'n'

mean of the ( Χ⁻ ) from the sample

level of significance z_{0.05} = 1.96 ( from z- tabulated value area at 0.95)

In this data we will use 95% of confidence intervals of the mean of the sample are given by

`(x^(-) - z_(0.05) (sigma)/(√(n) ) ,x^(-) + z_(0.05) (sigma)/(√(n) ))`

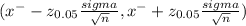
we will substitute given data

`(550- 1.96 (100)/(√(100) ) ,550+1.96 (100)/(√(100)))`

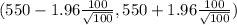
on simplification , we get

(530.4 ,569.6)

The 95% confidence intervals are (530.4 ,569.6) of sample means under the null hypothesis