Question

Is the mean weight of female college students still 59.4 kg? To test this, you take a random sample of 20 students, finding a mean of 61.65 kg with a standard deviation of 6.39 kg. Suppose the necessarily assumptions are satisfied, use a significance level of 0.10 to perform a significance test. A Fail to reject with 0.05 < P-value < 0.10. There is not sufficient evidence that the mean weight of female students has changed. B Fail to reject with 0.10 < P-value < 0.20. There is not sufficient evidence that the mean weight of female students has changed. C Reject with 0.05 < P-value < 0.10. There is sufficient evidence that the mean weight of female students has changed. D Reject with 0.10 < P-value < 0.20. There is sufficient evidence that the mean weight of female students has changed. E There is not enough information to perform the test.

Answer 1

Correct option: (B)

Explanation:

A one-sample t-test can be performed to determine whether the mean weight of female college students is still 59.4 kg.

The hypothesis can be defined as:

H₀: The mean weight of female college students has changed.

Hₐ: The mean weight of female college students has not changed.

The information provided is:

`\bar x=61.65\\s=6.39\\n=20\\\alpha =0.10`

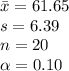
As the there is no information about the population standard deviation we will use a t-test for the mean.

The test statistic is:

`t=(\bar x-\mu)/(\s/√(n))=(61.65-59.4)/(6.39/√(20))=1.57`

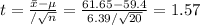
Decision rule:

If the if the p-value of the test is less than the significance level of the test α then the null hypothesis will be rejected and vice versa.

The degrees of freedom of the test is:

`df=n-1=20-1=19`

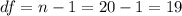
The test is two-tailed.

Compute the p-value of the test as follows:

`p-value=2* P(t_(0.10/2, 19)<1.57)=2* 0.065=0.13`

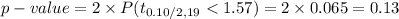
*Use a t-table for the probability.

The p-value = 0.13 > α = 0.10

The null hypothesis was failed to be rejected.

As the null hypothesis was rejected it can be concluded that there is not sufficient evidence that the mean weight of female students has changed.