Answer:
The initial velocity at which the ball is kicked is 9.22 m/s
Step-by-step explanation:
Given
bridge height, h = 36 m
Horizontal distance at which ball falls,
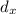 = 25 m
= 25 m
Firstly, we have to find the time taken by ball to reach vertically. It is calculated using formula,
d =
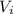 t +
t +

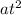
where d is vertical distance, d = h and a is acceleration due to gravity, a = g = 9.8 m/
 . Also initially ball is at rest, hence
. Also initially ball is at rest, hence
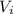 = 0. Substituting the values in the formula, we get
= 0. Substituting the values in the formula, we get
-36 = 0 +
 (-
(-
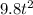 ) (negative sign is because the object moves downward)
) (negative sign is because the object moves downward)
 = 7.347
= 7.347
t =
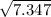
= 2.711 s
To find: initial velocity
We know that horizontal velocity is derived from horizontal distance and time:
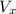 =
=
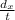
=
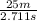
= 9.22 m/s