Question

An IQ test is designed so that the mean is 100 and the standard deviation is 2525 for the population of normal adults. Find the sample size necessary to estimate the mean IQ score of statistics students such that it can be said with 9999​% confidence that the sample mean is within 66 IQ points of the true mean. Assume that sigmaσequals=2525 and determine the required sample size using technology. Then determine if this is a reasonable sample size for a real world calculation.

Answer 1

The sample size must be 116 so that the sample mean is within 6 IQ points of the true mean.

Explanation:

We are given the following in the question:

Mean,
`\bar{x}` = 100

Alpha, α = 0.01

Population standard deviation, σ = 25

Margin of error = 6

We have to find the sample size such that the margin of error is 66.

Margin of error =

`z_(critical)* (\sigma)/(√(n))`

`z_(critical)\text{ at}~\alpha_(0.01) = 2.58`

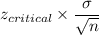
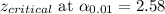
Putting values, we get,

`6 = 2.58* (25)/(√(n))\\\\√(n) = (2.58* 25)/(6)\\\\√(n) = 10.75\\n = 115.5625\approx 116`

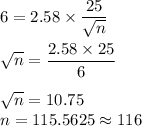
Thus, the sample size must be 116 so that the sample mean is within 6 IQ points of the true mean.

Yes, this is a reasonable sample size as it gives the required margin of error but it is a sairly large number.