Question

The sample mean x - = 18.15 exceeds 18, but perhaps this is only sampling error. Determine whether the data provide sufficient evidence, at the 10% level of significance, to conclude that the mean temperature for the entire day exceeds 18°C.

Answer 1

Explanation:

Hello!

One water quality standard for water that is discharged into a particular type of stream or pond is that the average daily water temperature be at most 18°C. Six samples taken throughout the day gave the data:

16.8, 21.5, 19.1, 12.8, 18.0, 20.7

The sample mean x−−=18.15 exceeds 18, but perhaps this is only sampling error. Determine whether the data provide sufficient evidence, at the 10% level of significance, to conclude that the mean temperature for the entire day exceeds 18°C.

The variable of interest is X: temperature of stream/pond water.

The average temperature of this water is supposed to be at most 18ºC but there is some concern that it might be greater.

Using the given data you have to test whether the true average temperature of the water is at most 18ºC or not, symbolically:

H₀: μ ≤ 18

H₁: μ > 18

α: 0.10

Assuming thas this variable has a normal distribution and considering the small sample, the statistic to use is a one-sample t-test:

`t= (X[bar]-Mu)/((S)/(√(n) ) ) ~~ t_(n-1)`

First you need to calculate the sample standard deviation

`S= \sqrt{(1)/(n-1)[sumX^2-((sumX)^2)/(n) ] }`

sumX= ∑X= 108.9

sum X²= ∑X²= 2025.63

`S= \sqrt{(1)/(5)[2025.63-((108.9)^2)/(6) ] }= 3.13`

`t_(H_0)= (18.15-18)/((3.13)/(√(6) ) ) = 0.12`

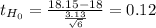
The p-value for this test is 0.4556

Decision rule using the p-value approach:

If p-value > α, do not reject the null hypothesis

If p-value ≤ α, reject the null hypothesis

⇒ The p-value is greater than α, the decision is to not reject the null hypothesis.

Critical value approach

This test is one-tailed to the right, the critical value is:

`t_(n-1;1-\alpha )= t_(5;0.90)= 1.476`

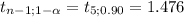
Decision rule:

If
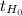`t_(H_0)` ≥ 1.476, reject the null hypothesis

If
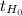`t_(H_0)` < 1.476, do not reject the null hypothesis

⇒ The calculated statistic is less than the critical value, the decision is to not reject the null hypothesis.

At a level of significance of 10%, there is no significant evidence to reject the null hypothesis. Then the average temperature of the water does no exceed 18ºC.

I hope you have a SUPER day!