Question

Based on data collected from metal shredders across the nation, the amount L of extractable lead in metal shredder residue has an approximate exponential distribution with mean μ = 2.0 milligrams per liter. What is the probability that L is greater than 1.20 milligrams per liter?

Answer 1

Probability that L is greater than 1.20 milligrams per liter is 0.5488.

Explanation:

We are given that based on data collected from metal shredders across the nation, the amount L of extractable lead in metal shredder residue has an approximate exponential distribution with mean μ = 2.0 milligrams per liter.

The probability distribution for exponential distribution is given by;

`f(l) = \lambda e^(-\lambda l) ; l >0`

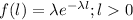
where,
`\lambda` = parameter of this distribution

Let L = Amount of extractable lead in metal shredder residue

Now, as we know that the mean of exponential distribution is;

Mean,
`\mu` =
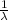`(1)/(\lambda)` ⇒ 2.0 =
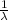`(1)/(\lambda)` {because we are given with the mean}

So,
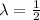`\lambda=(1)/(2)` = 0.5

Hence, L ~ Exp(
`\lambda = 0.5`)

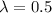Now, to find the less than or greater than probabilities in exponential distribution we use the Cumulative distribution function of exponential function, i.e.;

`F(L) = P(L \leq l) = 1 - e^(-\lambda l) ; l >0`

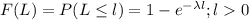
So, probability that L is greater than 1.20 milligrams per liter is given by = P(L > 1.20 milligrams per liter)

P(L > 1.20) = 1 - P(L
`\leq` 1.20)

= 1 - [
`1 - e^(-0.5 * 1.20)` ]

=
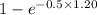`e^(-0.5 * 1.20)` = 0.5488

Therefore, probability that L is greater than 1.20 milligrams per liter is 0.5488.

Answer 2

`P(L >1.2)`

The cumulative distirbution function is given by:

`P(L <l) = 1-e^(-\lambda x)`

And using the complement rule we have:

`P(L>1.2) = 1-P(L<1.2) = 1-[1- e^{-(1.2)/(2)}] = e^{-(1.2)/(2)} = 0.549`

Explanation:

Previous concepts

The cumulative distribution function (CDF) F(x),"describes the probability that a random variableX with a given probability distribution will be found at a value less than or equal to x".

The exponential distribution is "the probability distribution of the time between events in a Poisson process (a process in which events occur continuously and independently at a constant average rate). It is a particular case of the gamma distribution". The probability density function is given by:

`P(X)=\lambda e^(-\lambda x)`

Solution to the problem

For this case we define the random variable L="the amount L of extractable lead in metal shredder residue" and the distirbution for X is given by:

`L \sim Exp( \lambda =(1)/(2)=0.5`

For this case we want this probability:

`P(L >1.2)`

The cumulative distirbution function is given by:

`P(L <l) = 1-e^(-\lambda x)`

And using the complement rule we have:

`P(L>1.2) = 1-P(L<1.2) = 1-[1- e^{-(1.2)/(2)}] = e^{-(1.2)/(2)} = 0.549`