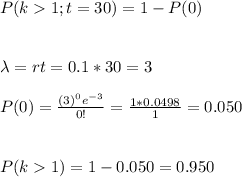Question

[Q9] The time between calls to a corporate office is exponentially distributed with a mean of 10 minutes. (a) What is the probability that there are more than three calls in one-half hour? (b) Given that in the first 15 minutes, there are no calls to the office. What is the probability that there will be (at least) one call in the next half hour?

Answer 1

a) P=0.353

b) P=0.950

Explanation:

If the time between calls is exponentially distributed with a mean rate of t minutes, we can say that the expected number of calls per unit of time follows a Poisson distribution with parameter 1/t.

In this case, the parameter for the Poisson distribution is:

`r=(1)/(10)=0.1\, min^(-1)`

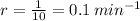
The Poisson distribution for k amount of calls in a period ot t minutes is described as:

`P(k,t)=((rt)^ke^(-rt))/(k!)`

The probability of having more than 3 calls in on-half hour (30 min) is:

`P(k>3;t=30)=1-(P(0)+P(1)+P(2)+P(3))\\\\\\ \lambda=rt=0.1*30=3\\\\P(0)=((3)^0e^(-3))/(0!) =(1*0.0498)/(1)=0.050\\\\P(1)=((3)^1e^(-3))/(1!)=(3*0.0498)/(1) = 0.149\\\\ P(2)=((3)^2e^(-3))/(2!)=(9*0.0498)/(2) = 0.224\\\\P(3)=((3)^3e^(-3))/(3!)=(27*0.0498)/(6) =0.224\\\\\\ P(k>3)=1-(0.050+0.149+0.224+0.224)\\\\P(k>3)=1-0.647=0.353`

b) These distribution are memory-less, so they are independent of the past results.

We can calculate then the probability of having at least on call in the next half hour as:

`P(k>1;t=30)=1-P(0)\\\\\\ \lambda=rt=0.1*30=3\\\\P(0)=((3)^0e^(-3))/(0!) =(1*0.0498)/(1)=0.050\\\\\\ P(k>1)=1-0.050=0.950`