Answer:
Wavelength of alpha particle is
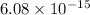 m
m
The de broglie wavelength of 1keV is 451 times larger than size of nucleus.
Step-by-step explanation:
Given:
Energy of alpha particle
 MeV
MeV
De broglie wavelength corresponding the energy of alpha particle is given by,
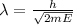
Where
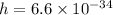 Js,
Js,
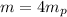 ,
,
 kg
kg

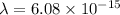 m
m
Hence, wavelength of alpha particle is
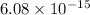 m
m
Size of nucleus is ≅
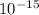 m
m
Now wavelength of 1 keV is given by,
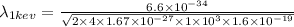
 m
m
Here,
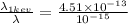 ≅ 451
≅ 451
Therefore, the de broglie wavelength of 1keV is 451 times larger than size of nucleus.