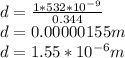Question

The reflective surface of a CD consists of spirals of equally spaced grooves. If you shine a laser pointer on a CD, each groove reflects circular waves that look exactly like the circular waves transmitted by the slits in a grating. You shine a green laser pointer (λ = 532 nm) perpendicularly to the surface of a CD and observe a diffraction pattern on a screen that is 3.0 m away from the CD. You observe that the 1st order maximum (m = 1) appears 1.1 m away from the central maximum (m = 1).

Determine the distance between the adjacent grooves on a CD.

Answer 1

d = 1.55 * 10⁻⁶ m

Step-by-step explanation:

To calculate the distance between the adjacent grooves of the CD, use the formula,
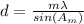`d = (m \lambda)/(sin(A_(m)) )`..........(1)

The fringe number, m = 1 since it is a first order maximum

The wavelength of the green laser pointer,
`\lambda` = 532 nm = 532 * 10⁻⁹ m

Distance between the central maximum and the first order maximum = 1.1 m

Distance between the screen and the CD = 3 m

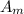`A_(m)` = Angle between the incident light and the diffracted light

From the setup shown in the attachment, it is a right angled triangle in which

`sin(A_(m)) = (opposite)/(Hypotenuse) \\sin(A_(m)) =\frac{1.1}{\sqrt{1.1^(2)+3^(2)}}`

`sin(A_(m) ) = 0.344\\A_(m) = sin^(-1) 0.344\\A_(m) = 20.14^(0)`

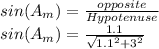
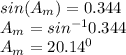
Putting all appropriate values into equation (1)

`d = (1* 532*10^(-9) )/(0.344 )\\d = 0.00000155 m\\d = 1.55 * 10^(-6) m`