Answer:
Explanation:
Hello!
You have the information of two samples taken from two different normal populations,
Sample 1
Steel: 107.1, 109.5, 107.4, 106.8, 108.1
X₁: work adhesion of ultra-high performance concrete to the steel substrate (mj/m²)
n₁= 5
X[bar]₁= 107.78
S₁²= 1.16
S₁= 1.08
Sample 2
Glass: 122.4, 124.6, 121.6, 120.6, 123.3
X₂: work adhesion of ultra-high performance concrete to the glass substrate (mj/m²)
n₂= 5
X[bar]₂= 122.50
S₂²= 2.37
S₂= 1.54
You need to test the claim that the mean work of adhesion for the glass substrate is more than 12 mj/m² higher than that for the steel substrate, i.e. that the difference between the mean work adhesion for the glass substrate and the mean work adhesion for the steel substrate is greater than 12 mj/m², symbolically: μ₂ - μ₁ > 12
Then the statistic hypotheses are:
H₀: μ₂ - μ₁ ≤ 12
H₁: μ₂ - μ₁ > 12
There is no significant level listed, I'll use 5%
Since both populations are normal and the sample sizes are quite small beside the population variances are unknown but can be assumed equal, you have to use a t-test for independent samples and pooled sample variance:
![t= \frac{(X[bar]2-X[bar]_1)(Mu_2-Mu_1)}{Sa*\sqrt{(1)/(n_2) +(1)/(n_1) } } ~~ t_(n_1+n_2-2)](https://img.qammunity.org/2021/formulas/mathematics/college/k6tvrhggkixmcqk6x0gh5i1cuxsyz4t8la.png)
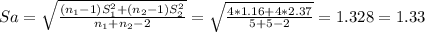

Using the critical value approach, this test is one-tailed to the right, which means that you will reject the null hypothesis at great values of t, the critical value is:
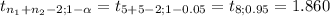
The deicision rule is:
If
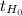 ≥ 1.860, you reject the null hypothesis
≥ 1.860, you reject the null hypothesis
If
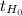 < 1.860, you do not reject the null hypothesis.
< 1.860, you do not reject the null hypothesis.
The calculated t-value is greater than the critical value, the decision is to reject the null hypothesis.
Using a significance level of 5% there is significant evidence to conclude that the true average work of adhesion for the glass substrate is more than 12 mj/m² higher than that for the steel substrate.
I hope you have a SUPER day!