Question

A journalist is planning to write an article about public opinion of gun control laws. He wants to poll 500 residents of a county in order to estimate what proportion of that population supports stricter gun laws. From the results of the poll, he plans to construct a 95% confidence interval. After calculating how much it would cost to contact 500 random residents, his supervisor tells him that it is too expensive, and that he has the budget to only contact 300 or fewer residents. a. What impact will the smaller sample size have on the width of the final confidence interval? b. Knowing that he must use a sample size of 300 or less, what is one thing the journalist can change in order to end up with a narrower interval?

Answer 1

a) The smaller sample size will result on a wider confidence interval.

b) You can decrease the confidence level.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`. The higher the confidence level, the higher the value of x.

The margin of error of the interval is:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

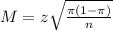
So as z increases, the interval gets wider. As z decreases, the interval gets narrower.

As n increases, the interval gets narrower. As n decreases, the interval gets wider.

a. What impact will the smaller sample size have on the width of the final confidence interval?

By the explanation above, the smaller sample size will result on a wider confidence interval.

b. Knowing that he must use a sample size of 300 or less, what is one thing the journalist can change in order to end up with a narrower interval?

You can decrease the confidence level.